Da nun durch diese imaginäre Zahl eine Lösung geschaffen war,
musste man sich diese Zahl auch irgendwie vorstellbar machen.
Bisher kannte man nur den gewöhnlichen Zahlenstrahl. Dieser Zahlenstrahl
wird nun durch die imaginären Zahlen nun um eine Ebene erweitert.
Dadurch sind die imaginären und reellen Zahlen darstellbar in einem rechtwinkligen
Koordinatensystem. Dieses nennt man die Gauß'sche Zahlenebene. Die reellen
Zahlen lassen sich auf der x-Achse finden und die imaginären Zahlen auf der
y-Achse.
So können reelle Zahlen wie Punkt A auf der x-Achse gefunden werden.
Imaginäre Zahlen lassen sich wie bereits erwähnt auf der y-Achse finden,
wie zum Beispiel Punkt B.
Komplexe Zahlen sind die Zahlen, die aus reellen und imaginären Zahlen bestehen,
also in der Abbildung die Punkte C, D und E.
Aus dem Koordinatensystem kann man entnehmen, dass alle komplexen Zahlen aus zwei
Koordinaten bestehen, somit ergibt sich (a;b), wobei a Realteil (reelle Zahl)
und b Imaginärteil (imaginäre Zahl) genannt werden.
Realteil und Imaginärteil einer komplexen Zahl werden in der Mathematik als
Realteil Re(z) einer komplexen Zahl z und Imaginärteil Img(z) einer komplexen
Zahl z bezeichnet.
Somit ergeben sich folgende Darstellung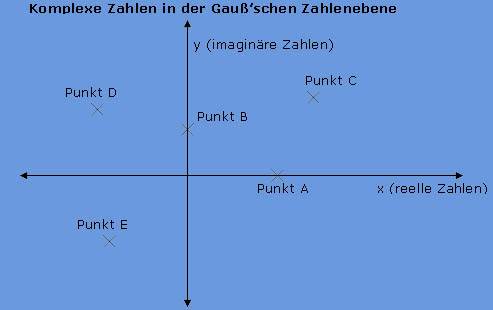en:
In dieser Abbildung lässt sich diese Darstellung erkennen. Die einzelnen Punkte
im Koordinatensystem lassen sich auch benennen.
(a;0): Reelle Zahlen
(0;b): Imaginäre Zahlen
(a;b): Komplexe Zahlen