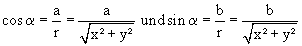Bei dieser Abbildung gilt
Der Winkel
Da
Da
Diese Form ist eine Darstellung in Polarkoordinatenform.
In dieser Form kann man ebenso jede reelle Zahl - wie auch schon in der
Gauß'schen Darstellungsform - darstellen:
Für jede positive reelle Zahl a gilt:
(Das Argument, welches die Ausrichtung auf der x-Achse nach links beschreibt,
ist
Weiterhin kann man zur einfacheren Rechnung für cos und sin folgende Zusammenhänge feststellen: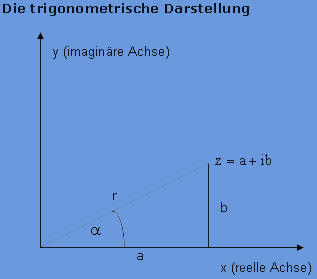
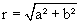, wobei gilt:
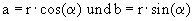
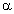wird Argument von z genannt.
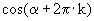sowie 
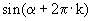für beliebige 
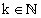gleich ist,
ist das Argument von z (arg z) nicht eindeutig bestimmt.
Dies ist der Fall bei Vielfachen von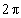 
,
die zum Argument addiert werden.
Die komplexe Zahl z=(0;0) kann nicht in der trigonometrischen Form dargestellt
werden, da ihr kein Argument eindeutig zugeordnet werden kann.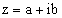
, gilt für die trigonometrische Darstellung folgendes:
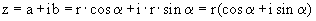
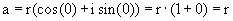, da
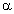gleich 0 sein muss, da jede reelle Zahl im Koordinatensystem auf der x-Achse
rechts des Ursprungs liegt. Für jede negative reelle Zahl gilt natürlich:
)
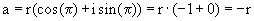
